INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA

En está entrada se pretende ensamblar los elementos estudiados en las entradas:  “La pendiente de rectas tangente y secantes”, “Cálculo del perímetro de un círculo a través de polígonos regulares”, “Noción intuitiva de límite” y “Notación, propiedades y procedimientos de obtención de límites”

con la intención de construir el concepto de derivada y su interpretación.

Aplicación de los límites en la obtención de la pendiente de la recta tangente a una curva.

Recordemos que la expresión de la pendiente de una recta

la hemos expresado como

donde h es diferente de cero.

Gráfica 1. Pendiente

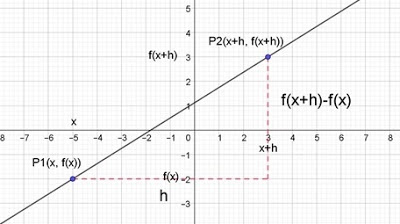
En nuestro estudio previo hemos visto que cuando desde un punto fijo de una curva trazamos rectas secantes (rectas que cortan a una curva en dos puntos) y vamos disminuyendo el valor de la diferencia de sus coordenadas en x hasta que está se aproxima a cero, la recta secante que se obtiene en ese proceso tiende a convertirse en la recta tangente a la curva en ese “punto fijo”. Esto es que el valor de h tiende a valer cero (x2-x1).

La gráfica siguiente refuerza lo que se pretende transmitir:

Gráfica 2. Secantes y tangente a una curva

Si al cociente

que determina la pendiente de una recta le aplicamos el concepto de límite que hemos venido estudiando, en este caso para cuando h tiende a cero tenemos:

 donde “m” es la pendiente de la recta tangente a la curva en un punto dado:

Concepto geométrico de la derivada

Geométricamente, a este límite lo conoceremos como la derivada de la función f(x).

Por tanto, podemos definir a la derivada, desde el punto de vista geométrico como la pendiente de la recta tangente a la curva en un punto dado.

Denotaremos a la derivada de una función f(x) como:

Ejemplo:

Determinar la derivada de la función:

Solución

La derivada (y’) será,

para nuestra función tenemos:

desarrollando el binomio al cuadrado tenemos:

realizando operaciones del numerador, nos queda:

factorizamos h en el polinomio del numerador

simplificamos eliminando tanto del numerado como del denominador la h. ¿Por qué las podemos eliminar?

obtenemos el límite

quedándonos

Teniendo la derivada de la función, ya podemos determinar el valor de la pendiente de la recta tangente a la curva en cualquier punto donde la curva exista. Por ejemplo, si se desea obtener la ecuación de la recta tangente a la curva

x = - 3 tenemos:

Como la derivada es igual a la pendiente de la recta tangente a la curva, en x = -3 tenemos:

Con el valor calculado de la pendiente y la ecuación punto pendiente de la recta

podemos conocer la ecuación de la recta tangente a la curva y=x² para x = -3, restándonos, únicamente, conocer el valor de y1 que se obtiene sustituyendo en la función el valor de x1. Así

Finalmente, aplicando a la expresión de la recta tangente a la curva en su forma punto pendiente tenemos:

La ecuación buscada de la recta es

A continuación, se presentan las gráficas de la curva y = x² y de recta 6x + y + 9 = 0

Videos de apoyo en la obtención de derivadas desarrollados por el profesor

Derivación por definición 01

Derivación por definición 02

Derivación por definición 03

No olvides participar en la sección de comentarios con dudas, hallazgos y cualquier otro aspecto relacionado con el tema aquí descrito. No olvides que un blog facilita el aprendizaje colectivo.