En esta entrada se pretende apoyar al lector en la
consecución de las competencias necesarias para determinar las pendientes y
ecuaciones de las rectas tangentes a una curva. Revistiendo esta competencia
una gran importancia para la aplicación del cálculo.
ELEMENTOS TEÓRICOS Y METODOLÓGICOS
Recordemos que la pendiente de una línea recta es una forma
de expresar la inclinación que presenta una recta. Esta inclinación se expresa
como el cociente de la variación que existe entre dos puntos de la variable
dependiente “y” entre la variación que sufre la variable independiente “x”. La
pendiente se denota con la letra “m”.
En el estudio de la interpretación geométrica de la derivada
hemos concluido que la pendiente de cualquier recta tangente a una curva es
igual a la derivada de esa curva. Así,
De esta manera, basta con obtener la derivada para poder
obtener la pendiente de cualquier recta tangente a una curva.
Para conocer la pendiente de la recta tangente a una curva en
cualquier punto de esta, debemos sustituir el valor de la variable
independiente en la derivada de la función de la curva y realizar las
operaciones que involucra, siendo el resultado del proceso la pendiente de la
recta tangente a la curva en el punto de interés.
Una vez que ya contamos con la pendiente de la recta tangente
a la curva en un punto dado, aplicamos el valor obtenido de la pendiente y las
coordenadas del punto de tangencia a la ecuación de la recta
Obteniendo con ello, tras las simplificaciones y arreglos
necesarios, la ecuación de la recta tangente a la curva en el punto
especificado.
EJEMPLOS
Los siguientes videos e imágenes ejemplifican el procedimiento
de obtención tanto de la pendiente como de la ecuación de la recta tangente a
una curva en un punto dado.
Ejemplo 1
Obtener la pendiente y la ecuación de la recta tangente a la
curva
para los puntos en que las coordenadas de la variable
independiente (x) son 2 y 3.
APLICACIONES DERIVADA. Obtención de la pendiente y
ecuación
de la recta tangente. Ejemplo 1
Ejemplo 2
Obtener la pendiente y la ecuación de la recta tangente a la
curva
para los puntos en que las coordenadas de la variable
independiente (x) son 1, 4 y 6.
APLICACIONES DERIVADA. Obtención de la pendiente y
ecuación
de la recta tangente. Ejemplo 2
EJERCICIOS PROPUESTOS
Realizar los ejercicios siguientes de obtención de la pendiente
y la ecuación de la recta tangente.
Es muy recomendable que participen en la sección de
comentarios con sus aportes, descubrimientos o dudas sobre el tema. Esta
sección permite el crecimiento de los participantes, tanto de los que aportan como
de los que aprenden de ellos.



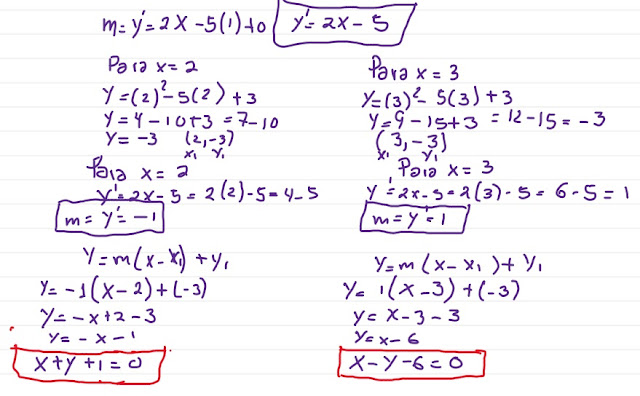


Alejandra Daimareli Gómez Zavala 4to A Recursos Humanos fue muy entendible ya que solo tenemos que sustituir en la ecuación inicial
ResponderBorrarlesly sugey flores aguirre 4*A
ResponderBorrarAdministración de Recursos Humanos
ALEJANDRA VIANEY TAPIA MEJIA 4A CONTABILIDAD
ResponderBorrarJonathan ángel Antolino Sepúlveda 4° A Electrónica T.M.
ResponderBorrarJulio Cesar Ruiz Yañez "4°A" Ofimática Matutino
ResponderBorrarAndrea Hernández Aguilar 4_A
ResponderBorrarAdministración de Recursos Humanos
Juan Carlos Cisneros Moreno 4°A Ofimatica Matutino
ResponderBorrarMelany Andrea Lerma Castillo
ResponderBorrar4°A Administración de Recursos Humanos
Leslie Azul Martínez Luqueño
ResponderBorrar4°"A" Ofimática
Kimberly michel Calvillo rivera 4-A ofimática
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarVanessa Monter Garcia 4"A OFIMATICA
ResponderBorrarYovana Guadalupe Acosta Alcantar
ResponderBorrar4°A Administración de Recursos Humanos
Dylan Josué Díaz Orozco 4°A Electrónica
ResponderBorrarÁngel Francisco Guzmán Saldaña
ResponderBorrar4A Ofimática
Alicia Morelia Jaimes Ortiz
ResponderBorrar4A Contabilidad
Hugo Miguel Villa Rodriguez 4-A Ofimática
ResponderBorrarEdson González García/Electrónica/ 4°A
ResponderBorrarJohana Saenz Salinas 4°"A" OFIMATICA
ResponderBorrarMitzi Guadalupe Corona Rosas
ResponderBorrarOfimática 4A
Ángel David Hernández Torres ofimática 6°A
ResponderBorrarAlejandra TovarMuñoz 4°A Administración de Recursos Humanos
ResponderBorrarAndrea Lucas Mejia 4-A Administracion de Recursos Humanos
ResponderBorrarJulio Osvaldo Guzmán Correa Electrónica 4_A
ResponderBorrarYahir Facio Rodriguez 4°A Ofimatica
ResponderBorrarDylan Alejandro Sandoval Estrada
ResponderBorrar4°A Contabilidad