LA PENDIENTE DE RECTAS SECANTES Y TANGENTES

Base fundamental para el estudio del cálculo diferencial

En esta entrada se presenta el estudio de los elementos mencionados en el título y su importancia en la comprensión y estudio del cálculo diferencial. Analizamos sus relaciones y propiedades para establecer una expresión de la pendiente que servirá de base para la construcción del concepto de derivada.

Recta secante a una curva

Recordemos de Geometría Analítica que una recta secante a una curva es aquella recta que corta a dicha curva en dos puntos. Las siguientes imágenes muestran ejemplos de rectas secantes a una curva.

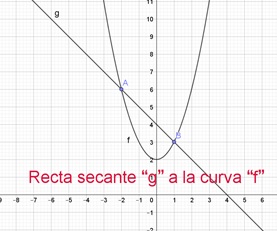
La recta secante “g” corta a la curva “f” en los puntos A(-2, 6) y B(1, 3).

La recta secante “g” corta a la curva “f” en los puntos A(-1, -1) y B(0,0)

Preguntas de reforzamiento:

1. Cuál es el signo de la pendiente de la recta secante a la curva mostrada en la imagen del lado izquierdo?

2. ¿Cuál es el signo de la pendiente de la recta secante a la curva mostrada en la imagen del lado derecho?

3 ¿Cuál es la expresión que se utiliza para calcular la pendiente de una recta cuando se conocen dos puntos de ella?

4. Calcula la pendiente de ambas rectas y verifica si el signo corresponde a las respuestas que diste en los dos primeros incisos.

Recta tangente a una curva

A diferencia de la recta secante, una recta tangente a una curva es aquella que la toca en un solo punto. En las siguientes imágenes se muestran ejemplos de rectas tangentes a una curva.

La recta tangente “g” toca únicamente a la recta “f” en el punto (1, -2)

La recta tangente “g” toca a la curva “f” en el punto A(1, 3)

Preguntas de reforzamiento:

1. ¿Cuál es el signo de la pendiente de la recta secante a la curva mostrada en la imagen del lado izquierdo?

2. ¿Cuál es el signo de la pendiente de la recta secante a la curva mostrada en la imagen del lado derecho?

3. ¿Cuál es la expresión que se utiliza para calcular la pendiente de una recta cuando se conocen dos puntos de ella?

4. Calcula la pendiente de ambas rectas y verifica si el signo corresponde a las respuestas que diste en los dos primeros incisos.

Pendiente de una recta

En geometría analítica, la pendiente de una recta se define como la inclinación que esta presenta con respecto de la horizontal. La pendiente se simboliza con la letra “m” y se expresa, tomados dos puntos de la recta, como el cociente de la diferencia en los valores de la variable independiente “y” entre la diferencia de los valores de la variable dependiente “x”, considerando los signos de dichas diferencias. Así, considerando los puntos P1(x₁, y₁) y P2(x₂, y₂):

Para los fines del cálculo diferencial, introduciremos una notación diferente, ella nos permitirá avanzar en el estudio de este campo de las matemáticas. Consideremos la gráfica siguiente:

En esta última gráfica hemos cambiado, únicamente, los nombres generalizados de las coordenadas. Las coordenadas del punto 1 las denominamos x y f(x), en tanto que, las coordenadas del punto 2 serán (x+h, f(x+h)). Donde h, es la diferencia en los valores de la variable independiente (x) de los dos puntos analizados. No olvidemos que el valor de la pendiente de una recta dada no depende de los puntos que tomemos para su cálculo, este siempre es el mismo para cualquier par de puntos (la inclinación de una recta particular es la misma siempre).

Ahora pasemos de la expresión de la pendiente utilizada en Geometría Analítica 

a la que emplearemos en cálculo diferencial

Donde h debe ser diferente de 0. ¿Por qué?

Nota 1:

Para mayor comprensión revisa las dos últimas gráficas hasta que la equivalencia en expresiones te quede clara.

Nota 2:

En gran cantidad de libros, revistas o medios donde se estudia el cálculo diferencial, se emplea Δx en lugar de h. Δx se lee, “delta x”. Δ es un símbolo que en matemáticas se utiliza para representar cambios en los valores de una variable. La expresión nos quedaría:

Relación basada en la pendiente de las rectas tangentes y secantes a una curva.

Observemos la siguiente secuencia de imágenes en que, el valor de h ( de la recta secante disminuye de tal forma que está tiende a convertirse en la recta tangente a la curva en el punto (x, fx(x))

El punto inferior ha permanecido fijo y el superior se ha venido recorriendo en la curva hasta que ambos coinciden (revisar las imágenes en la secuencia indicada). Cuando ambos puntos coinciden, la recta secante a la curva que pasa por el punto fijo “A”, se convierte en la recta tangente a la curva en ese punto. Este hallazgo es de suma importancia en la comprensión y aplicación del cálculo diferencial.

Ejemplos de cálculo del cociente 

Para h diferente de cero de las siguientes funciones:

Para favorecer el aprendizaje del tema, en la parte de los comentarios pueden compartir dudas, descubrimientos, materiales y cualquier otro tipo de información que resulte útil para este esfuerzo académico.