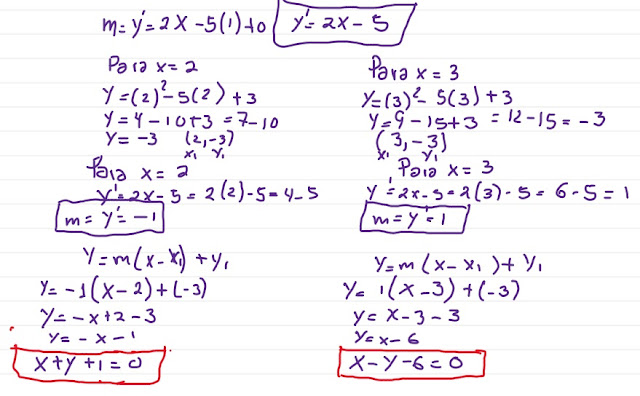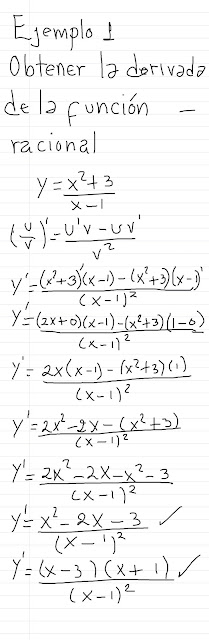En esta entrada se pretende apoyar al lector en la
consecución de las competencias necesarias para determinar las pendientes y
ecuaciones de las rectas tangentes a una curva. Revistiendo esta competencia
una gran importancia para la aplicación del cálculo.
ELEMENTOS TEÓRICOS Y METODOLÓGICOS
Recordemos que la pendiente de una línea recta es una forma
de expresar la inclinación que presenta una recta. Esta inclinación se expresa
como el cociente de la variación que existe entre dos puntos de la variable
dependiente “y” entre la variación que sufre la variable independiente “x”. La
pendiente se denota con la letra “m”.
En el estudio de la interpretación geométrica de la derivada
hemos concluido que la pendiente de cualquier recta tangente a una curva es
igual a la derivada de esa curva. Así,
De esta manera, basta con obtener la derivada para poder
obtener la pendiente de cualquier recta tangente a una curva.
Para conocer la pendiente de la recta tangente a una curva en
cualquier punto de esta, debemos sustituir el valor de la variable
independiente en la derivada de la función de la curva y realizar las
operaciones que involucra, siendo el resultado del proceso la pendiente de la
recta tangente a la curva en el punto de interés.
Una vez que ya contamos con la pendiente de la recta tangente
a la curva en un punto dado, aplicamos el valor obtenido de la pendiente y las
coordenadas del punto de tangencia a la ecuación de la recta
Obteniendo con ello, tras las simplificaciones y arreglos
necesarios, la ecuación de la recta tangente a la curva en el punto
especificado.
EJEMPLOS
Los siguientes videos e imágenes ejemplifican el procedimiento
de obtención tanto de la pendiente como de la ecuación de la recta tangente a
una curva en un punto dado.
Ejemplo 1
Obtener la pendiente y la ecuación de la recta tangente a la
curva
para los puntos en que las coordenadas de la variable
independiente (x) son 2 y 3.
APLICACIONES DERIVADA. Obtención de la pendiente y
ecuación
de la recta tangente. Ejemplo 1
Ejemplo 2
Obtener la pendiente y la ecuación de la recta tangente a la
curva
para los puntos en que las coordenadas de la variable
independiente (x) son 1, 4 y 6.
APLICACIONES DERIVADA. Obtención de la pendiente y
ecuación
de la recta tangente. Ejemplo 2
EJERCICIOS PROPUESTOS
Realizar los ejercicios siguientes de obtención de la pendiente
y la ecuación de la recta tangente.
Es muy recomendable que participen en la sección de
comentarios con sus aportes, descubrimientos o dudas sobre el tema. Esta
sección permite el crecimiento de los participantes, tanto de los que aportan como
de los que aprenden de ellos.